提示您，本文原题为 -- 陶哲轩等式的一个新证法

摘要：陶哲轩教授在[1]中分别利用 Cauchy- Binet型公式和伴随矩阵两种方法证明了一个关于埃尔米特（Hermite）矩阵的特征根 ， 特征向量中的元素及其子矩阵特征根之间关系的一个等式 。 本文利用分块矩阵的方法对此等式给出一个更直接更简洁的新证明 。

最近网上都在热议三位物理学家向著名数学天才陶哲轩教授求证一个关于矩阵及其子矩阵的特征根与特征向量元素之间的一个关系式 ， 出于好奇 ， 我们在网上找到了这篇文献 ， 读过之后发现我们还可以给出一个更简洁更直接的新证明 。

设 A 是一个埃尔米特（Hermite）矩阵 ， 具有特征根和赋范的特征向量 ， 每个特征向量中的元用表示 。 设是 A 的一个（n-1) x (n-1) 子矩阵 ， 它是通过删去 A 的第 j 行和第 j 列的所有元 ， 保持其余元不动而得到的矩阵 ， 它的特征根用表示 。 作为[1]的主要结果 ， 陶哲轩教授分别利用 Cauchy- Binet 型公式和伴随矩阵两种方法证明了下述结果 。

定理 0.1. 设 A 是一个 m 阶埃尔米特矩阵 ， 则下面等式成立

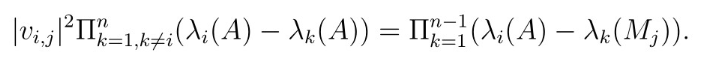
陶哲轩等式的一个新证法// //

证明. 见 [1, Lemma2 ] 。

由于特征根是相似不变量 ， 如[1]指出 ， 证明上述关于 A 的等式等价证明关于矩阵 A —的相应等式 ， 从而可假定为零 ， 并取i=n, j=1, 而使上面等式有下列约化形式

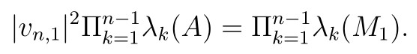
陶哲轩等式的一个新证法// //

我们在本文实际上取i=n, j=n ， 证明了下述约化形式

由于也是一个埃尔米特矩阵 ， 故 。 我们基于[2]的第九章第 8 节的结果和符号 ， 证明了上述等式 。

定理 0.2. 设 A 是一个n阶埃尔米特矩阵 ， 且其特征根, 则 。

证明. 因为 A 是一个n阶埃尔米特矩阵 ， 故存在n阶酉矩阵U使得是个对角矩阵 ， 并且可设 。 可设

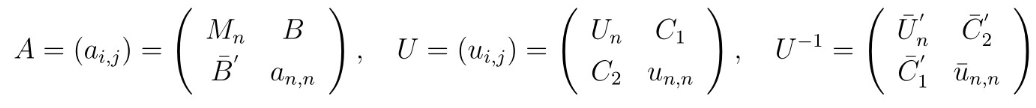
陶哲轩等式的一个新证法// //

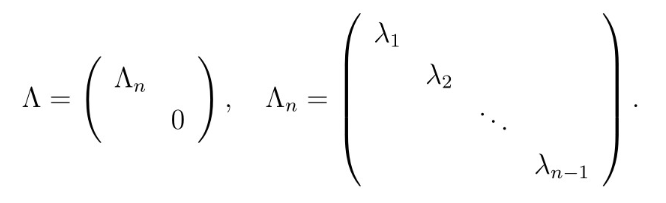
陶哲轩等式的一个新证法// //

可得

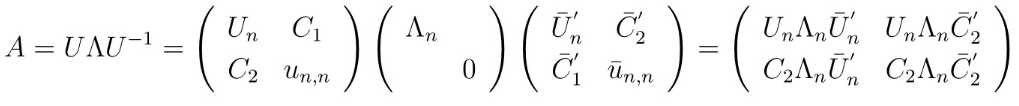
陶哲轩等式的一个新证法// //

进而得 ， 所以 ， 故只需证明足矣 ， 注意到 。

因为 U 是酉矩阵 ， 可得

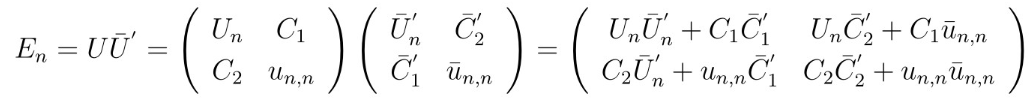
陶哲轩等式的一个新证法// //

故得 。 进而得 。 上述等式中 ， 最后一个等号是因为 。 倒数第二个等号可利用[2] p203习题29的结果 。 因此 。 证毕 。

参考文献

[1] P.B.Denton, S.J.Parke, T.Tao, and X.Zhang, Eigenvectors from eigenvalues, arXiv: 1908. 03795 v[math RA], 10 Aug 2019.

[2] 王萼芳 ， 石生明 ， 高等代数（第三版） ， 高等教育出版社 ， 2003.

编辑 ∑Gemini

• 八雅轩丨【墨缘有约】曹宝麟：学好书法，我有十条建议
• 【梅轩夜读】胡适日记抄之二十三：胡适这样一个留学生为什么娶了不识字的江冬秀？
• 四川三苏祠式苏轩遗址发掘首次发现宋代遗址 出土遗物500件
• 皮实耐用还不贵！朗逸轩逸如何选？
• 八雅轩丨【墨缘有约】古人为何爱用“斋”来命名自己的书房？
• 德藩最乐轩：刻书十数，《汉书》尤名（上）韦力撰
• 好书推荐 | 国际安徒生奖得主曹文轩首部侦探小说，带你在悬疑中探问复杂人性！
• 别解轩辕、颛顼
• 懋勤轩三迤掌故：大宋提刑官发明的《尸格》
• 轩辕黄帝诞生的故事：自古少女爱英雄，感天动地怀龙种