Berry curvature的积分为何为2π整数倍?
提示您,本文原题为 -- Berry curvature的积分为何为2π整数倍?
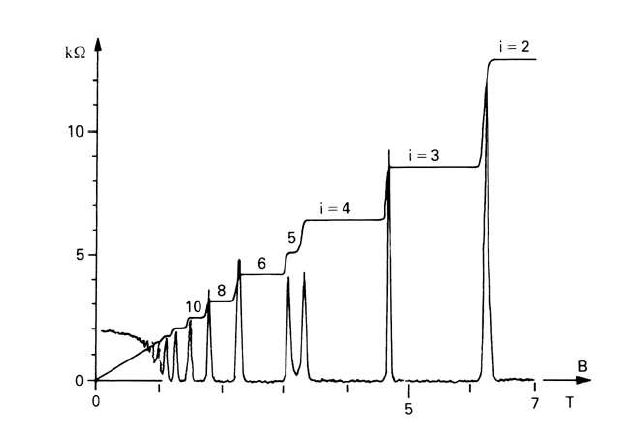
之前讨论了整数量子霍尔效应
Berry curvature的积分为何为2π整数倍?// //
弱磁场的情况下 , 非对角的霍尔电导和磁场强度满足经典的线性关系 , 强磁场作用下出现了很多量子化Hall的平台 , 其 Hall conductance 正比 Berry curvature在Brillouin zone的积分 ,
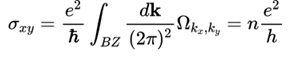
Berry curvature的积分为何为2π整数倍?// //
其中Berry curvature和Berry connection为
Hall conductance的量子化平台取决于这个积分
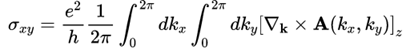
Berry curvature的积分为何为2π整数倍?// //
叉乘展开并作个分布积分可得
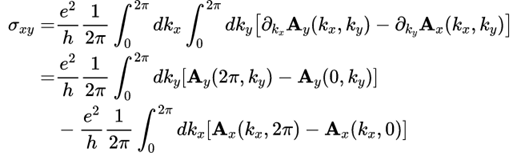
Berry curvature的积分为何为2π整数倍?// //
等价于看Berry connection在0和2π的变化的积分 , 由于周期性边界条件的限制 , 0和2π处的波函数只相差一个phase
有
类似的有
代入Hall conductance可得
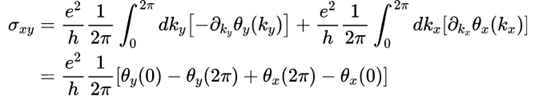
Berry curvature的积分为何为2π整数倍?// //
且有边界条件
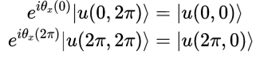
Berry curvature的积分为何为2π整数倍?// //
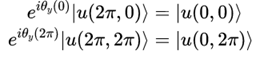
Berry curvature的积分为何为2π整数倍?// //
可得
即
从而证明了Berry curvature积分是2π的整数倍以及Hall conductance的量子化 , 也证明了拓扑不变量Chern number ( first Chern number也叫TKNN number) 必须是整数
1. SHUN-QING. SHEN. Topological Insulators: Dirac Equation in Condensed Matter. Springer, 2018.
推荐阅读
- 齐白石画山水:懂的人不多,骂的人却不少
- 一个人的长征:追寻孙子
- 晋朝电视剧为何只拍到司马炎登基统一三国,以后的事情为何不拍?
- 《圣斗士星矢》重病的伊利亚斯为什么还能对冥斗士产生重大威胁?
- 凿壁偷光的匡衡,后来怎样了?成了贪官为害一方
- 古代最有钱的县城大街,位于山西,现为世界遗产!
- 小脚的起源:为防疫古人如何解决大妈们串门、扎堆的问题
- 元宵节的由来与传说
- 自编教材评审的标准是什么
- 曹操有14个老婆,12个是抢来的寡妇,一代枭雄为何爱抢人妻?









